|
On cherche à étudier les forces intérieures qui agissent sur le viaduc de Millau et ainsi justifier la présence et l’assemblage des différents éléments de la construction, en particulier les haubans.
Pour cela, on va étudier ce qui se passerait si les haubans n’étaient pas en place.
On réalise tout d’abord un schéma du viaduc, en le représentant plus simplement comme s’il n’avait que trois piles et on
réalise le bilan des forces.
_ à Référentiel : la Terre (Galiléen)
_ à Système : {Le viaduc de Millau}
_ à Bilan des forces : - le Poids de la charge du tablier
- le Poids de la surcharge du tablier
- la Résistance des piles
Les forces du poids s’appliquent sur tout le tablier, celle de la résistance au point de contact entre le tablier et la pile.
On fait ainsi une modélisation du viaduc :
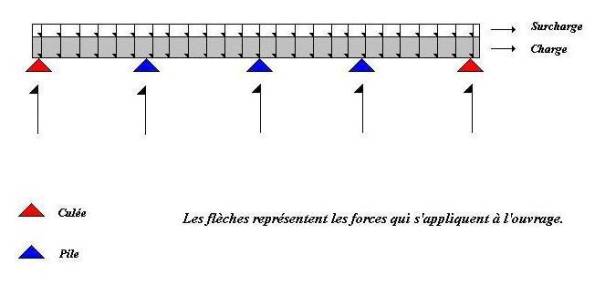
Maintenant, assimilons le viaduc à une poutre qui reposerait sur plusieurs points fixes. Le poids des charges étant très élevé, on assisterait sans doute à un fléchissement de la poutre entre les piles :
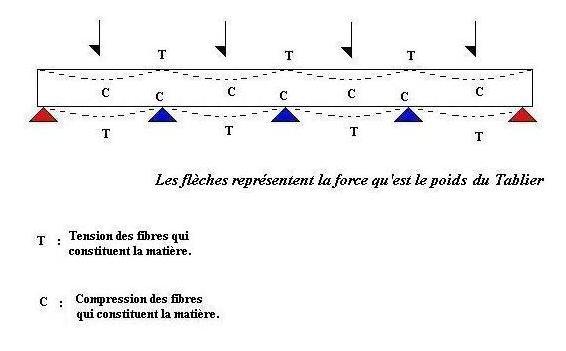
On constate ainsi un fléchissement entre les piles. La matière
étant constituée de fibres, on observe une tension des
fibres inférieures et une compression des fibres supérieures
qui abîmeraient très rapidement la matière et donc le
viaduc. Afin de résoudre ce problème, on trace la représentation
graphique du mouvement fléchissant C : m(x).
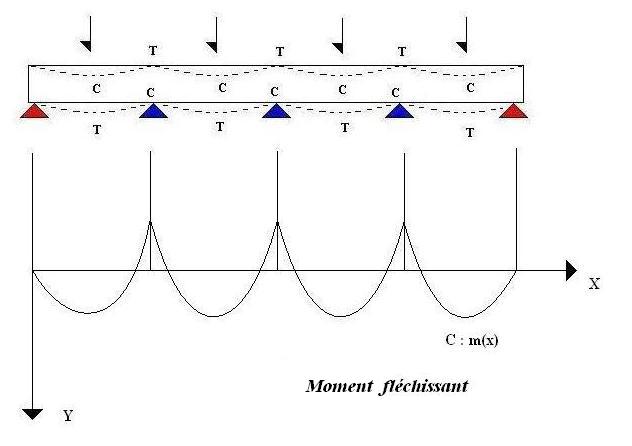
On se propose d’étudier la fonction représentée par la première partie de la courbe. On trouve ainsi
:
m(x) = - 100x² + 19 200x
m(x) s’exprime alors en m.kN. (Cliquez ici pour accéder au raisonnement mathématique permettant de trouver la fonction).
Les parties de la courbe sont ainsi proportionnelles au risque de fléchissement du tablier
aux points concernés. On remarque que le risque est le plus grand au milieu des segments délimités par les piles (les perpendiculaires sur le graphique).
On constate aussi qu’au niveau des piles, le moment fléchissant est négatif. Il s’agit en fait d’un moment inverse consécutif à la force de résistance des piles par opposition aux autres moments
fléchissant.
Enfin pour étudier ce moment, on trace aussi la courbe de l’effort tranchant qui se trouve être la dérivée du moment fléchissant C’ :
v(x) = m’(x) = -200x + 19
200
Cette courbe permet d’étudier les risques de cassure d’un point du tablier en fonction de la distance le séparant du point fixe le plus proche est s’exprime en kN.
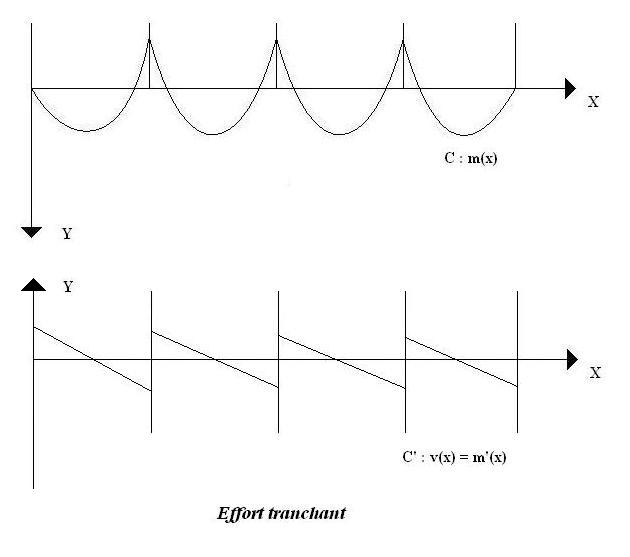
On s’aperçoit ainsi que les risques de cassure sont plus élevés près des pylônes. Où les risques apparaissent comme critiques. (Cliquez ici pour accéder aux valeurs remarquables de la première partie de la courbe).
Il apparaît donc indispensable de soutenir le tablier pour ne pas qu’il casse ou même fléchisse. C’est pour cela que les haubans sont mis en place. Ceci justifie bien l’axe longitudinal des haubans (identique à celui du viaduc et non normal à ce dernier) ainsi que ses fixations : les haubans sont fixés sur les pylônes et agissent sur tout le tablier mais rencontrent leurs voisins entre les segments délimités par les piles ce qui favorise l’opposition au mouvement fléchissant.

|