|
Nous
allons maintenant étudier la forme particulière des piles
qui a pour but de résister aux contraintes s’exerçant sur
le viaduc. Pour cela, nous allons considérer la pile P2, qui
est la plus haute et la plus spectaculaire des sept piles.

Ce
n’est pas une pile uniforme de haut en bas. En effet, à
environ 100 m du bas, elle se dédouble. Cependant le logiciel
que nous utilisons ne nous permettant pas d’étudier les
forces d’une telle structure, nous considèrerons qu’il
s’agit d’une pile uniforme dont voici les plans vu de
dessous :
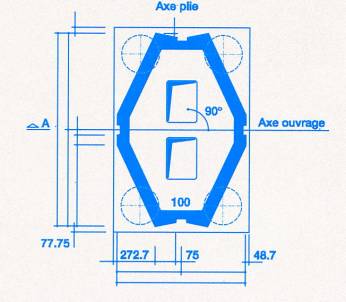
Nous constatons
qu’il ne s’agit en réalité pas d’un polygone parfait
mais d’une structure bien particulière et symétrique lui
permettant de mieux résister aux pressions exercées par le
vent dans cette région "houleuse".
Nous expliquons ceci de
deux manières complémentaires :
·
Tout d’abord, on explique l’aspect allongé
de la pile par sa meilleure prise au vent. En effet la
pression exercée par le vent sur le pilier, est consécutive
à l’accélération que doit avoir le vent pour contourner
l’obstacle qu’est la pile. Plus l’obstacle est grand,
plus le vent doit accélérer pour le contourner, plus les
risques de dépression et de formation de mini tornade sont élevés.
Ainsi, le fait de construire des piles allongées plutôt
qu’hexagonales favorise la prise au vent et évite les dépressions
qui risqueraient de faire basculer les piles ou bien de les
faire trop osciller.
Mais
l’obstacle est bel est bien toujours présent et des dépressions
se forment par conséquent au niveau des piliers. Pour y remédier,
les ingénieurs ont donc choisi de construire des piles
parfaitement symétriques afin que les dépressions se
compensent de chaque côté de la pile et que cette dernière
évite alors de bouger.
·
Mais il existe une autre raison pour expliquer cette forme et
cette orientation des piles.
En effet, l’inertie de la pile joue un rôle très
important dans sa formation.
L’inertie d’un objet se calcule à partir du plan normal
à cet objet : il s’agit d’une valeur mesurant le
risque que l’objet se casse.
Par exemple, si on assimile la pile P2 à une pile à base
rectangulaire, on obtient alors une hauteur h et une base b à
cette figure en sachant que les forces qui s’exercent sur
l’objet (en l’occurrence le vent) ont toujours une
direction perpendiculaire à la base :
L’inertie se calcule selon la formule suivante : (bh3)/12
et s’exprime en m4.
De cette façon, plus l’inertie est élevée, plus le risque
de cassure est faible et inversement.
On expliquerait ceci plus facilement à notre échelle en
prenant un double décimètre. Il est bien évident que
suivant le côté que l’on considère comme la base il y a
beaucoup plus de chance de cassure dans un cas que dans
l‘autre :
Il apparaît ici bien évident que les risques de casse sont
bien plus grands dans le premier cas que dans le deuxième.
Ceci vient de l’inertie de la règle :
(b2h23)/12
> (b1h13)/12
Ainsi,
on comprend bien la forme de la pile P2 qui a ainsi une
inertie beaucoup plus grande que si elle était de forme
hexagonale ou positionnée dans l’autre sens.
On
constate donc que les effets du vent sur les piles ont du être
un problème majeur lors de la construction du viaduc qui a été
résolu par la forme dont elle dispose aujourd’hui.
On se rend
compte que le viaduc est soumis à de nombreuses contraintes
qu’il est important d’étudier avant sa construction.
Toutes ces contraintes sont principalement physiques et consécutives
aux forces s’opposant au viaduc que la taille ne favorise
pas. Le viaduc de Millau apparaît ainsi comme une prouesse
technologique tant par sa taille que par la qualité des études
qui ont été faites à son propos.

|