|
On se propose d’étudier le moment fléchissant du tablier entre la culée C0 et la pile P1
Pour cela on défini tout d’abord les longueurs suivantes :
- l = longueur séparant C0 et P1 l = 240 m
- p = poids du tablier par répartition de masse c'est-à-dire à la force qu’exerce 1 m du tablier dur les piles (en kN.m-1).
Calcul de p :
La masse totale du tablier (comprenant le tablier, les pylônes et ls haubans) est de 41
100 t. En tenant compte de la surcharge (poids des véhicules, neige
éventuelle, eau), on arrondi cette valeur à 50 000 t soit 50 000 000 kg.
P = mg ≈ 50 000 000*10 = 500 000 000 N = 500 000 kN
Le tablier ayant une longueur de 2460 m, on obtient p = P/2460 ≈ 200 kN.m-1.
On modélise ensuite la partie du viaduc concernée :
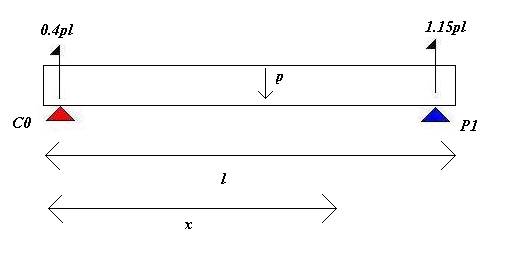
N’ayant pas la capacité de le démontrer on considèrera que la résistance opposé à la culée est de 0.4pl N est celle de la pile P1 de 1.15 N.
Ici x représente la distance qui sépare le point dont on cherche le moment fléchisseur de la culée C0. On considère que x est l’abscisse du point dont on recherche l’ordonnée sur la courbe dont on cherche l’équation :

On cherche maintenant à trouver son équation :
Le moment, étant dans le sens contraire aux réactions de la culée et de la pile, et s’exerçant sur la distance x, on obtient –px comme première action
Or la force obtenue s’exerce au milieu du segment x soit x/2.
On obtient donc comme facteur principal –px²/2
Or la force exercée par la culée C0 agit elle aussi sur x. Il faut donc ajouté 0.40plx.
On obtient donc une fonction :
m(x) = -px²/2 + 0.40 plx
d’où : m(x) = - 100x² + 19 200x
On observe enfin quelques valeurs remarquables :
- Le moment fléchissant au niveau de la culée C0 est m(0) = 0 kN.m
- Le moment fléchissant au niveau de la pile P1 est :
m(l) = - px²/2 + 0.4 plx = - 0.5 pl² +0.4 pl² = -0.10 pl² = -11 520 000 kN.m
- On cherche ensuite le moment fléchissant maximal. Pour cela on cherche la dérivée :
m’(x) = - 200x + 19200.
m’(x) est une fonction affine donc elle s’annule et change de signe où m(x) admet un maximum.
La courbe admet donc un maximum en x1 tel que
m’(x1) = 0 soit x1 = 19200/200 = 96m
- On cherche enfin à connaître les valeurs de x pour lesquelles le moment fléchissant est nul.
D’où
m(x) = 0 <=> -100x² + 19 200x = 0
<=> x (-100w +19 200) = 0
<=> x’ = 0 ou x’’= 192
Ainsi pour
x = 0 ou
x = 192 , le moment fléchissant est nul et au niveau des piles, il est négatif.
|